Tras varios meses desde que leí el libro sobre geometría sagrada de S. Skinner, he decidido recopilar mis notas y reflexiones acerca de todo lo que dicho libro me mostró. No voy a hacer como en otras ocasiones, un resumen del libro o voy a dar mi opinión fundamental sobre temas que pueden ser ampliamente tratados en libros como el leído, sino que quiero tratar de exponer mi opinión personal y apostillar en la medida que me sea posible lo que de manera somera lo indicado en el libro.
Lo principal es conocer el porqué de las proporciones divinas o como a mi me gusta más llamarlas “proporciones universales”. El estudio del número áureo, el número pi o el número e lo inicié como la mayoría de HH.·. en la época de la E.G.B. y lo amplié durante los años de B.U.P. Lo primero que nos enseñaron en dibujo de 8º de EGB fue a dibujar un Nautilus, un crustáceo prehistórico, con E.·., Cartabón, regla y C.·…. qué iniciación más adecuada, posteriormente nos enseñaron que aquella relación entre la diagonal de un cuadrado y el rectángulo dándonos a conocer que a partir de ella se formaba era el número áureo, una proporción utilizada en el arte y la construcción desde tiempos ancestrales. A través de aquello, y gracias a una extraordinaria profesora, en bachillerato descubrí el problema de la cuadratura del círculo con una simple regla y un compás. Ahora volviendo a leer el libro de Skinner, he retomado este problema geométrico que lejos de alejarme de la solución me acerca al conocimiento, el camino
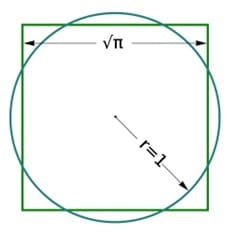

es lo importante; volviendo, de este modo, a enfrentarme a la temida raíz de pi. Este problema geométrico es la cadena de unión entre los antiguos geómetras y los modernos matemáticos, de la escuela pitagórica hasta nuestros días pasando por los más grandes como Rafael. ¿Por qué hago alusión a la cuadratura del círculo? Porque creo que es la conexión entre lo divino y lo humano, el conocimiento primordial y nuestro conocimiento limitado, sencillamente seguimos adelante en su búsqueda porque sabemos que es posible y que ese conocimiento existe. Aritméticamente fácil de comprobar, pero geométricamente todavía por resolver.
En la documentación que he leído, aparte del libro, sobre geometría sagrada siempre se hace alusión a la sucesión de Fibonacci, la proporción áurea y el orden en la naturaleza como signo de lo divino que nos rodea. Esto puede ser así y de hecho la teoría del Caos nos muestra que partiendo de un punto inicial podemos obtener sucesiones arbitrarias pero sujetas al mismo patrón, como sucede con los fractales, pero también puede degenerar y dar lugar a sucesiones exponenciales no replicables, esto es el Caos. Por tanto, no hemos de perder de vista nuestro suelo ajedrezado, el blanco y el negro, ya que si las condiciones iniciales no son las necesarias, obtendremos un resultado degenerado y caótico. Lo importante de todos estos patrones naturales y proporciones es que el G.·.A.·.D.·.U.·. ha dotado al hombre de la percepción necesaria para identificarlos y creo de manera fervorosa que todos y cada uno de nosotros los identificamos de manera subconsciente. Una prueba de ello son las representaciones de pinturas rupestres, la mayoría guardan las proporciones naturales de las imágenes representadas; esto quiere decir que la mente humana es capaz de reproducir lo que ve y por tanto el fuego alquímico que hay en nosotros nos permite representar las proporciones tal y como las percibimos o como Dios las concibió. Otro ejemplo que a mi me impresiona sobremanera es el de Vincent Van Gogh, quien dibujó de manera exacta cascadas de turbulencia definidas siglos más tarde por Kolmogorov. Las escalas de turbulencia no son más que la definición de la pérdida de energía en la turbulencia, el mejor ejemplo es un penacho de humo de cigarro en el que al principio las volutas de humo son enormes y luego se van descomponiendo en volutas cada vez más pequeñas debido a la pérdida de energía del fluido; esta descomposición y el tamaño de los torbellinos es exacto y depende del fluido y las condiciones iniciales. Sin embargo, Van Gogh sin conocer nada de esto fue capaz de representar en cuadros como “La Noche” una perfecta escala de turbulencia. Esto para mi, es la prueba de que el ser humano es capaz de asimilar y analizar todo lo que nos rodea y por ende portamos ese conocimiento primordial o secreto que hemos buscado desde el inicio de los tiempos. No debemos hacer pues otra cosa que buscar dentro de nosotros para encontrar el camino a ese conocimiento.


Del mismo modo que la geometría está presente en la naturaleza, lo terrenal, la aritmética está presente en las ideas, lo divino, y por tanto toda representación de geometría ha de tener su explicación matemática o aritmética. En este sentido, la evolución del conocimiento de la geometría ha ayudado también al avance del conocimiento de la aritmética y así mismo a otras ciencias como la física. Este es un tema que desde mi punto de vista el autor del libro propuesto en nuestra bibliografía no aborda con la profundidad necesaria. Conceptos matemáticos como la nada, la unidad, la dualidad o la numerología en general forman parte también de la geometría sagrada o de los templos conservados hasta hoy en día. Un claro ejemplo es la utilización del número 8, símbolo de lo infinito en las construcciones orientales que llegan hasta occidente a través de ordenes como los templarios o directamente a través de la arquitectura árabe en la Península Ibérica. No hemos de olvidar que la arquitectura árabe está fuertemente influenciada por los conocimientos geométricos derivados de los conocimientos que en la antigua Grecia se recopilaron. No fue sino a través de ellos por lo que resurgió el estudio de la cultura griega en Europa a través de Al-Andalus.
El inicio del libro si que me ha resultado interesante por el hecho de reflejar cómo se trataban los estudios matemáticos en el mundo antiguo, cómo transmitían el conocimiento las escuelas pitagóricas. Conceptos de aritmética fundamental o cómo se realizaban las medidas en aquella época en la que el sistema decimal todavía no se utilizaba, son temas en los que me gustaría profundizar en lecturas posteriores.
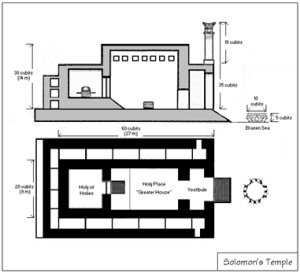
Sin entrar en la parte dedicada a la geometría de las catedrales, la parte que más ha llamado mi atención del estudio de la geometría sagrada es el concerniente a las dimensiones del templo del Rey Salomón.